Run a full experiment for comparing multiple algorithms using multiple instances

Design and run a full experiment - calculate the required number of instances, run the algorithms on each problem instance using the iterative approach based on optimal sample size ratios, and return the results of the experiment. This routine builds upon calc_instances() and calc_nreps(), so refer to the documentation of these two functions for details.

run_experiment(
  instances,
  algorithms,
  d,
  se.max,
  power = 0.8,
  sig.level = 0.05,
  power.target = "mean",
  dif = "simple",
  comparisons = "all.vs.all",
  alternative = "two.sided",
  test = "t.test",
  method = "param",
  nstart = 20,
  nmax = 100 * length(algorithms),
  force.balanced = FALSE,
  ncpus = 2,
  boot.R = 499,
  seed = NULL,
  save.partial.results = NA,
  load.partial.results = NA,
  save.final.result = NA
)

Arguments

instances: list object containing the definitions of the available instances. This list may (or may not) be exhausted in the experiment. To estimate the number of required instances, see calc_instances(). For more details, see Section Instance List.
algorithms: a list object containing the definitions of all algorithms. See Section Algorithms for details.
d: minimally relevant effect size (MRES), expressed as a standardized effect size, i.e., "deviation from H0" / "standard deviation". See calc_instances() for details.
se.max: desired upper limit for the standard error of the estimated difference between pairs of algorithms. See Section Pairwise Differences for details.
power: (desired) test power. See calc_instances() for details. Any value equal to or greater than one will force the method to use all available instances in Instance.list.
sig.level: family-wise significance level (alpha) for the experiment. See calc_instances() for details.
power.target: which comparison should have the desired power? Accepts "mean", "median", or "worst.case" (this last one is equivalent to the Bonferroni correction).
dif: type of difference to be used. Accepts "perc" (for percent differences) or "simple" (for simple differences)
comparisons: type of comparisons being performed. Accepts "all.vs.first" (in which cases the first object in algorithms is considered to be the reference algorithm) or "all.vs.all" (if there is no reference and all pairwise comparisons are desired).
alternative: type of alternative hypothesis ("two.sided" or "less" or "greater"). See calc_instances() for details.
test: type of test to be used ("t.test", "wilcoxon" or "binomial")
method: method to use for estimating the standard errors. Accepts "param" (for parametric) or "boot" (for bootstrap)
nstart: initial number of algorithm runs for each algorithm. See Section Initial Number of Observations for details.
nmax: maximum number of runs to execute on each instance (see calc_nreps()). Loaded results (see load.partial.results below) do not count towards this maximum.
force.balanced: logical flag to force the use of balanced sampling for the algorithms on each instance
ncpus: number of cores to use
boot.R: number of bootstrap resamples to use (if method == "boot")
seed: seed for the random number generator
save.partial.results: should partial results be saved to files? Can be either NA (do not save) or a character string pointing to a folder. File names are generated based on the instance aliases. Existing files with matching names will be overwritten. run_experiment() uses .RDS files for saving and loading.
load.partial.results: should partial results be loaded from files? Can be either NA (do not save) or a character string pointing to a folder containing the file(s) to be loaded. run_experiment() will use .RDS file(s) with a name(s) matching instance aliases. run_experiment() uses .RDS files for saving and loading.
save.final.result: should the final results be saved to file? Can be either NA (do not save) or a character string pointing to a folder where the results will be saved on a .RDS file starting with CAISEr_results_ and ending with 12-digit datetime tag in the format YYYYMMDDhhmmss.

Value

a list object containing the following fields:

Configuration - the full input configuration (for reproducibility)
data.raw - data frame containing all observations generated
data.summary - data frame summarizing the experiment.
N - number of instances sampled
N.star - number of instances required
total.runs - total number of algorithm runs performed
instances.sampled - names of the instances sampled
Underpowered - flag: TRUE if N < N.star

Instance List

Parameter instances must contain a list of instance objects, where each field is itself a list, as defined in the documentation of function calc_nreps(). In short, each element of instances is an instance, i.e., a named list containing all relevant parameters that define the problem instance. This list must contain at least the field instance$FUN, with the name of the problem instance function, that is, a routine that calculates y = f(x). If the instance requires additional parameters, these must also be provided as named fields. An additional field, "instance$alias", can be used to provide the instance with a unique identifier (e.g., when using an instance generator).

Algorithm List

Object algorithms is a list in which each component is a named list containing all relevant parameters that define an algorithm to be applied for solving the problem instance. In what follows algorithms[[k]] refers to any algorithm specified in the algorithms list.

algorithms[[k]] must contain an algorithms[[k]]$FUN field, which is a character object with the name of the function that calls the algorithm; as well as any other elements/parameters that algorithms[[k]]$FUN requires (e.g., stop criteria, operator names and parameters, etc.).

The function defined by the routine algorithms[[k]]$FUN must have the following structure: supposing that the list in algorithms[[k]] has fields algorithm[[k]]$FUN = "myalgo", algorithms[[k]]$par1 = "a" and algorithms[[k]]$par2 = 5, then:


         myalgo <- function(par1, par2, instance, ...){
               #
               # <do stuff>
               #
               return(results)
         }

That is, it must be able to run if called as:


         # remove '$FUN' and '$alias' field from list of arguments
         # and include the problem definition as field 'instance'
         myargs          <- algorithm[names(algorithm) != "FUN"]
         myargs          <- myargs[names(myargs) != "alias"]
         myargs$instance <- instance

         # call function
         do.call(algorithm$FUN,
                 args = myargs)

The algorithm$FUN routine must return a list containing (at least) the performance value of the final solution obtained, in a field named value (e.g., result$value) after a given run. In general it is easier to write a small wrapper function around existing implementations.

Initial Number of Observations

In the general case the initial number of observations / algorithm / instance (nstart) should be relatively high. For the parametric case we recommend 10~15 if outliers are not expected, and 30~40 (at least) if that assumption cannot be made. For the bootstrap approach we recommend using at least 15 or 20. However, if some distributional assumptions can be made - particularly low skewness of the population of algorithm results on the test instances), then nstart can in principle be as small as 5 (if the output of the algorithm were known to be normal, it could be 1).

In general, higher sample sizes are the price to pay for abandoning distributional assumptions. Use lower values of nstart with caution.

Pairwise Differences

Parameter dif informs the type of difference in performance to be used for the estimation ($\mu_a$ and $\mu_b$ represent the mean performance of any two algorithms on the test instance, and $mu$ represents the grand mean of all algorithms given in algorithms):

If dif == "perc" and comparisons == "all.vs.first", the estimated quantity is: $\phi_{1b} = (\mu_1 - \mu_b) / \mu_1 = 1 - (\mu_b / \mu_1)$.
If dif == "perc" and comparisons == "all.vs.all", the estimated quantity is: $\phi_{ab} = (\mu_a - \mu_b) / \mu$.
If dif == "simple" it estimates $\mu_a - \mu_b$.

Sample Sizes for Nonparametric Methods

If the parameter `` is set to either Wilcoxon or `Binomial`, this routine approximates the number of instances using the ARE of these tests in relation to the paired t.test:

n.wilcox = n.ttest / 0.86 = 1.163 * n.ttest
n.binom = n.ttest / 0.637 = 1.570 * n.ttest

References

F. Campelo, F. Takahashi: Sample size estimation for power and accuracy in the experimental comparison of algorithms. Journal of Heuristics 25(2):305-338, 2019.
P. Mathews. Sample size calculations: Practical methods for engineers and scientists. Mathews Malnar and Bailey, 2010.
A.C. Davison, D.V. Hinkley: Bootstrap methods and their application. Cambridge University Press (1997)
E.C. Fieller: Some problems in interval estimation. Journal of the Royal Statistical Society. Series B (Methodological) 16(2), 175–185 (1954)
V. Franz: Ratios: A short guide to confidence limits and proper use (2007). https://arxiv.org/pdf/0710.2024v1.pdf
D.C. Montgomery, C.G. Runger: Applied Statistics and Probability for Engineers, 6th ed. Wiley (2013)
D.J. Sheskin: Handbook of Parametric and Nonparametric Statistical Procedures, 4th ed., Chapman & Hall/CRC, 1996.

Author

Felipe Campelo (fcampelo@ufmg.br, f.campelo@aston.ac.uk)

Examples

# Example using four dummy algorithms and 100 dummy instances.
# See [dummyalgo()] and [dummyinstance()] for details.
# Generating 4 dummy algorithms here, with means 15, 10, 30, 15 and standard
# deviations 2, 4, 6, 8.
algorithms <- mapply(FUN = function(i, m, s){
  list(FUN   = "dummyalgo",
       alias = paste0("algo", i),
       distribution.fun  = "rnorm",
       distribution.pars = list(mean = m, sd = s))},
  i = c(alg1 = 1, alg2 = 2, alg3 = 3, alg4 = 4),
  m = c(15, 10, 30, 15),
  s = c(2, 4, 6, 8),
  SIMPLIFY = FALSE)

# Generate 100 dummy instances with centered exponential distributions
instances <- lapply(1:100,
                    function(i) {rate <- runif(1, 1, 10)
                                 list(FUN   = "dummyinstance",
                                      alias = paste0("Inst.", i),
                                      distr = "rexp", rate = rate,
                                      bias  = -1 / rate)})

my.results <- run_experiment(instances, algorithms,
                             d = .5, se.max = .1,
                             power = .9, sig.level = .05,
                             power.target = "mean",
                             dif = "perc", comparisons = "all.vs.all",
                             ncpus = 1, seed = 1234)
#> CAISEr running
#> -----------------------------
#> Required number of instances: 58
#> Available number of instances: 100
#> Using 1 cores.
#> -----------------------------
#> Sampling algorithms on instance Inst.28 : ..
#> Sampling algorithms on instance Inst.80 : ..
#> Sampling algorithms on instance Inst.22 : ..
#> Sampling algorithms on instance Inst.9 : ..
#> Sampling algorithms on instance Inst.5 : ..
#> Sampling algorithms on instance Inst.38 : ..
#> Sampling algorithms on instance Inst.16 : ..
#> Sampling algorithms on instance Inst.4 : ..
#> Sampling algorithms on instance Inst.86 : ..
#> Sampling algorithms on instance Inst.90 : ..
#> Sampling algorithms on instance Inst.70 : ..
#> Sampling algorithms on instance Inst.79 : ..
#> Sampling algorithms on instance Inst.78 : ..
#> Sampling algorithms on instance Inst.14 : ..
#> Sampling algorithms on instance Inst.56 : ..
#> Sampling algorithms on instance Inst.62 : ..
#> Sampling algorithms on instance Inst.93 : ..
#> Sampling algorithms on instance Inst.84 : .
#> Sampling algorithms on instance Inst.21 : .
#> Sampling algorithms on instance Inst.40 : .
#> Sampling algorithms on instance Inst.92 : .
#> Sampling algorithms on instance Inst.67 : .
#> Sampling algorithms on instance Inst.96 : .
#> Sampling algorithms on instance Inst.66 : .
#> Sampling algorithms on instance Inst.47 : .
#> Sampling algorithms on instance Inst.81 : .
#> Sampling algorithms on instance Inst.48 : .
#> Sampling algorithms on instance Inst.3 : .
#> Sampling algorithms on instance Inst.41 : .
#> Sampling algorithms on instance Inst.32 : .
#> Sampling algorithms on instance Inst.42 : .
#> Sampling algorithms on instance Inst.43 : .
#> Sampling algorithms on instance Inst.2 : .
#> Sampling algorithms on instance Inst.54 : .
#> Sampling algorithms on instance Inst.49 : .
#> Sampling algorithms on instance Inst.99 : .
#> Sampling algorithms on instance Inst.51 : .
#> Sampling algorithms on instance Inst.6 : .
#> Sampling algorithms on instance Inst.77 : .
#> Sampling algorithms on instance Inst.29 : .
#> Sampling algorithms on instance Inst.71 : .
#> Sampling algorithms on instance Inst.85 : .
#> Sampling algorithms on instance Inst.57 : .
#> Sampling algorithms on instance Inst.8 : .
#> Sampling algorithms on instance Inst.26 : .
#> Sampling algorithms on instance Inst.17 : .
#> Sampling algorithms on instance Inst.58 : .
#> Sampling algorithms on instance Inst.91 : .
#> Sampling algorithms on instance Inst.60 : .
#> Sampling algorithms on instance Inst.76 : .
#> Sampling algorithms on instance Inst.98 : .
#> Sampling algorithms on instance Inst.35 : .
#> Sampling algorithms on instance Inst.72 : .
#> Sampling algorithms on instance Inst.94 : .
#> Sampling algorithms on instance Inst.73 : .
#> Sampling algorithms on instance Inst.50 : .
#> Sampling algorithms on instance Inst.10 : .
#> Sampling algorithms on instance Inst.45 : .

# Take a look at the results
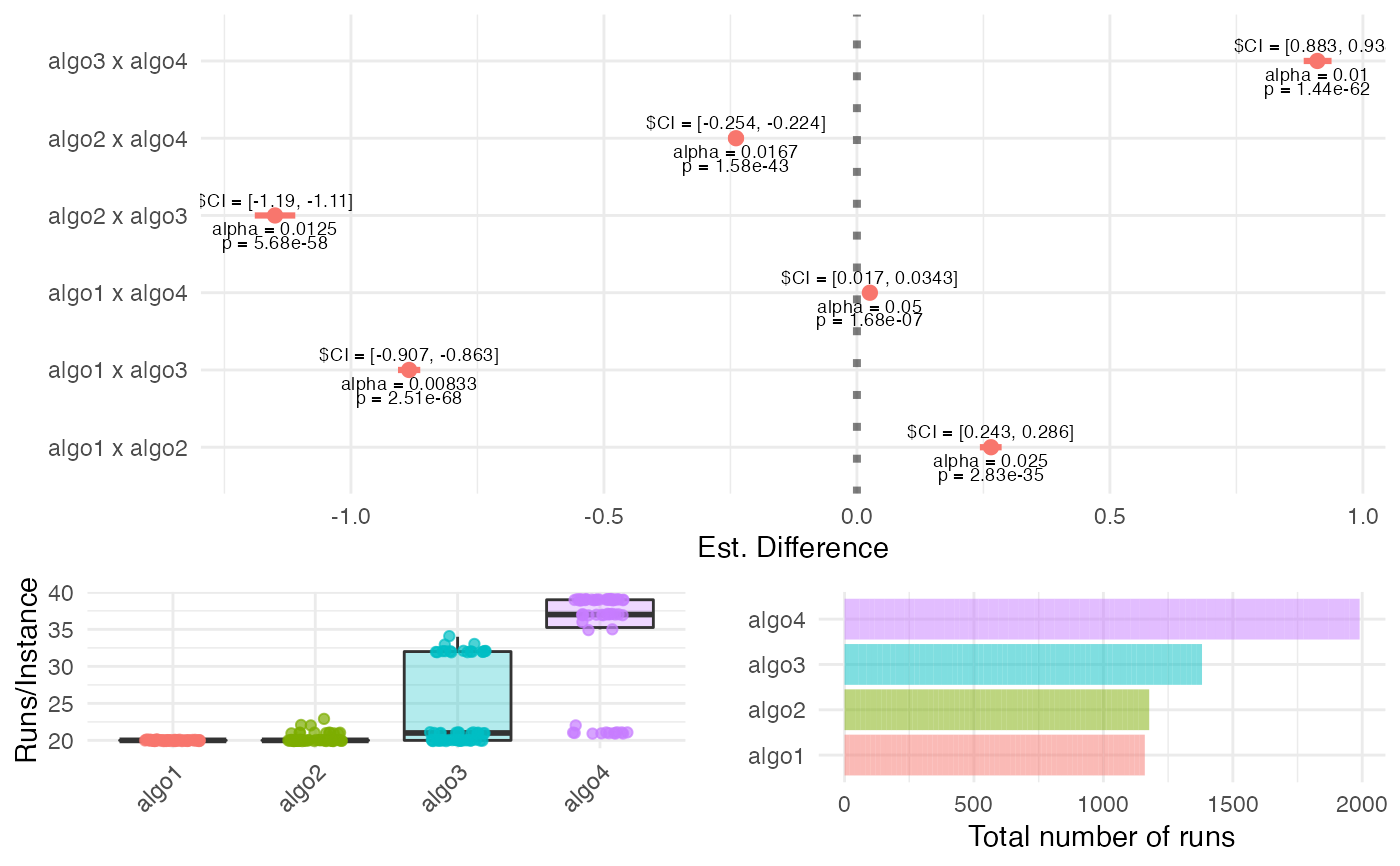
summary(my.results)
#> #====================================
#>  CAISEr object:
#>  Number of instances sampled: 58
#>  Number of instances required: 58
#>  Adequate power: TRUE
#>  Total runs of algo1 : 1160
#>  Total runs of algo2 : 1177
#>  Total runs of algo3 : 1381
#>  Total runs of algo4 : 1990
#> #====================================
#>  Pairwise comparisons of interest:
#>  Test: t.test
#>  H1: two.sided
#>  Comparisons: all.vs.all
#>  Alpha (FWER): 0.05
#>  Power target: mean
#>  Desired power: 0.9
#> #====================================
#> Tests using Holm's step-down procedure:
#> 
#>  Test 1 : algo1 x algo3
#>  H0: mean = 0
#>  alpha		= 0.008333 
#>  p-value	= 2.512e-68
#>  Est. mean	= -0.8848
#>  CI{1-alpha}	= [ -0.9065 -0.863 ]
#>  d		= -14.58974
#> 
#>  Test 2 : algo3 x algo4
#>  H0: mean = 0
#>  alpha		= 0.01 
#>  p-value	= 1.445e-62
#>  Est. mean	= 0.9104
#>  CI{1-alpha}	= [ 0.8828 0.938 ]
#>  d		= 11.54558
#> 
#>  Test 3 : algo2 x algo3
#>  H0: mean = 0
#>  alpha		= 0.0125 
#>  p-value	= 5.682e-58
#>  Est. mean	= -1.149
#>  CI{1-alpha}	= [ -1.19 -1.109 ]
#>  d		= -9.574107
#> 
#>  Test 4 : algo2 x algo4
#>  H0: mean = 0
#>  alpha		= 0.01667 
#>  p-value	= 1.58e-43
#>  Est. mean	= -0.2389
#>  CI{1-alpha}	= [ -0.2536 -0.2242 ]
#>  d		= -5.279244
#> 
#>  Test 5 : algo1 x algo2
#>  H0: mean = 0
#>  alpha		= 0.025 
#>  p-value	= 2.828e-35
#>  Est. mean	= 0.2645
#>  CI{1-alpha}	= [ 0.243 0.286 ]
#>  d		= 3.719929
#> 
#>  Test 6 : algo1 x algo4
#>  H0: mean = 0
#>  alpha		= 0.05 
#>  p-value	= 1.68e-07
#>  Est. mean	= 0.02564
#>  CI{1-alpha}	= [ 0.01702 0.03425 ]
#>  d		= 0.782428
#> #====================================
plot(my.results)